Lens Distortion (렌즈 왜곡) 효과를 영상 처리로 구현 하는 또 다른 방법(Inverse Mapping)을 정리하고, WPF OpenCV 프로젝트에 추가해 보겠습니다. 이전 포스팅(#26)에서 다룬 Lens Distortion(렌즈 왜곡) 효과는 사실 포토샵의 Liquify(픽셀 유동화)나 어안 렌즈 효과 처럼 사용자가 원하는 지점을 중심으로 이미지를 볼록하거나, 오목하게 만드는 기능이었습니다.
볼록/오목 효과를 이미지의 특정 좌표를 기준으로 직교 좌표를 획득해서, 극 좌표로 변환하고, 왜곡 연산 후 다시 직교 좌표 데이터를 사용하여 구현 했었죠. 이번 포스팅에서는 그 구현 방식을 조금 더 깊이 파고들어, “왜 이렇게 구현해야 하는가?”에 대한 Optimization (최적화) 관점과 Inverse Mapping (역방향 매핑)의 수학적 원리를 조금 상세히 정리해 보겠습니다. (그냥 수학적 표현이니 너무 어려워 하지 않았으면 좋겠네요.)
그리고 단순히 기능을 만드는 것을 넘어, 메모리를 아끼고 속도를 높이는 방법도 조금 다루겠습니다.
Manual Calculation
지난 포스팅에서 Lens Distortion 을 구현하면서 OpenCV의 cv::cartToPolar나 cv::polarToCart 같은 편리한 함수들을 활용했습니다. 그런데 왜 굳이 지금 와서 복잡한 수식을 써가며 직접 계산하려 할까요?
OpenCV 함수 사용 시의 문제점 (메모리 낭비)
기존 방식대로 OpenCV 함수들을 조합하면 다음과 같은 과정이 필요합니다.
- 모든 좌표 행렬 생성
CartToPolar실행 Magnitude(), Angle() 행렬 생성 (메모리 할당)- 값을 왜곡(Power)
PolarToCart실행 새로운 행렬 생성 (메모리 할당)
위와 같은 처리 과정에서 중간 계산을 위한 임시 행렬(Magnitude, Angle 등)이 계속 생성되고 해제됩니다. 고해상도 이미지라면 메모리 사용량이 급증하고, Cache Hit Rate (캐쉬 적중률)이 떨어져 속도가 느려질 수 있습니다.
Manual Calculation
앞서 언급한 문제점을 해결하는 방법은 메모리 사용량을 급증 시키는 중간 행렬을 만들지 않고, 픽셀 하나를 처리할 때 즉석에서 좌표를 변환하고 왜곡해버리면 됩니다. 그리고, 하나 하나 기다리지 말고 이것을 Parallel.For를 이용해 병렬로 처리하여 극한의 성능을 뽑아 낸다면 정말 좋겠죠!
Inverse Mapping : 역방향 매핑
Remap 함수를 사용할 때 가장 중요한 개념은 역방향 매핑입니다.
- 정방향 (Forward): “원본의 (10, 10) 픽셀 너는 (12, 12)로 이동해라.” (다만 구멍이 생길 수 있음)
- 역방향 (Inverse): “결과 화면의 (12, 12) 픽셀 너는 원본의 (10, 10)에서 색깔을 가져와라.” (구멍이 안 생김)
이렇게 결과 이미지의 모든 픽셀 () 을 순회하면서, “이 픽셀은 원본의 어디()에서 가져와야 하지?” 를 계산해서 mapX, mapY에 기록하도록 하는 것입니다.
Mathematical Concept
자, 이제 보기만 해도 짜증 나는 수식이 등장하지만 괜찮을 겁니다. 왜냐면 아주 논리적이 거든요.
중심 점 기준 상대 좌표 구하기
이미지의 왼쪽 위(0,0)가 아닌, 사용자가 클릭한 중심점(Center)을 (0,0)으로 생각해야 합니다.
극 좌표 변환 (거리 계산)
핏 덩어리 시절에 배웠던 피타고라스의 정리를 이용해 중심점에서 현재 픽셀까지의 거리()를 구합니다.
Normalization : 거리 정규화
만약 거리가 픽셀 단위(예: 500px)면 계산이 복잡하므로, 전체 이미지 크기 대비 비율()로 변경 합니다. 이것이 바로 정규화된 반지름() 이 됩니다.
Distortion : 왜곡 적용
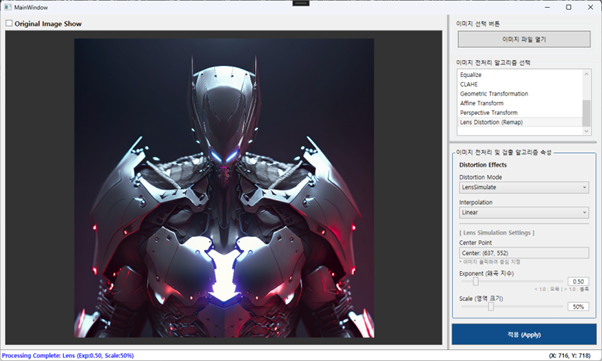
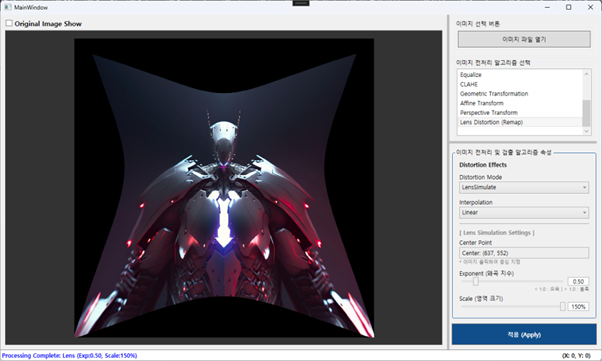
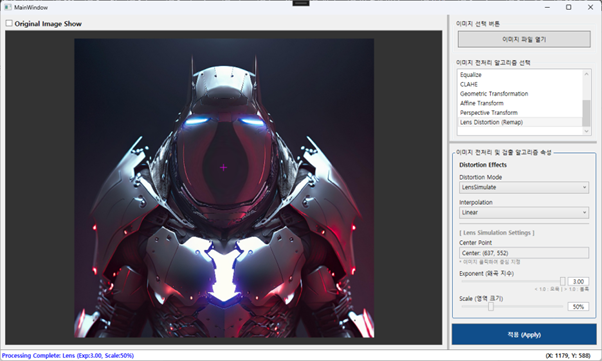
이제 앞서 구한 거리를 왜곡 시켜야 합니다. 지수()가 1보다 크면 거리가 짧아져서(가져오는 위치가 중심에 가까워짐) 확대(볼록) 효과가 나고, 1보다 작으면 축소(오목) 효과가 이미지에 적용됩니다.
Scale Factor : 스케일 비율
Manual Calculate 의 가장 중요한 부분이 여기인데요, 각도를 다시 계산(atan2)하고 cos, sin을 곱하는 것은 연산 비용이 너무 비쌉니다. 대신에 “거리가 얼마나 늘어났는가?” 에 대한 비율만 알 수 있으면 됩니다..
Original Coordination : 원본 좌표 복원
비율을 까지 알았으니까, 아까 구한 상대 좌표()에 비율만 곱해주면 원본 위치가 나옵니다. 삼각함수(sin, cos)를 쓰지 않아서 속도가 훨~씬 빠릅니다.
구현
이번 포스팅에서는 구현 요약이 필요하지 않습니다. 지난 포스팅에 추가되었던 대부분의 내용 즉 UI(view), Model, ViewModel 코드들을 대부분 그대로 사용하니까요. 수정해야 하는 부분은 딱 한군데~ 바로 OpenCVService.cs 파일에서 영상 처리를 구현하는 함수인 ProcessImageAsync() 함수 인데요. 기존 switch 구문에서 case “Lens Distortion (Remap)”: 아래의 코드를 위에서 정리한 수학적 개념을 그대로 가져가면 됩니다. 위의 수학적 개념을 코드로 구현 부분은 아래와 같아요. 한번 천천히 따라가 보도록 하세요. 어렵지 않을 겁니다.
case "Remap":
if (parameters is RemapParams rParams)
{
if (rParams.Mode == RemapMode.LensSimulate)
{
// 1. 매핑 테이블 생성 (32bit float)
Mat mapX = new Mat(_srcImage.Size(), MatType.CV_32FC1);
Mat mapY = new Mat(_srcImage.Size(), MatType.CV_32FC1);
// 포인터 접근 대신 안전하고 빠른 제네릭 인덱서 사용 (또는 포인터 사용 가능)
var indexerX = mapX.GetGenericIndexer<float>();
var indexerY = mapY.GetGenericIndexer<float>();
int w = _srcImage.Width;
int h = _srcImage.Height;
double cx = rParams.CenterX * w; // 중심점 X
double cy = rParams.CenterY * h; // 중심점 Y
double exp = rParams.Exponent; // 왜곡 지수
// 최대 반지름 (정규화를 위해 필요, 대각선 길이의 절반 등)
double maxRadius = Math.Sqrt(w * w + h * h) / 2.0;
// 2. 병렬 루프 (Parallel.For) - 성능 최적화의 핵심
Parallel.For(0, h, y =>
{
for (int x = 0; x < w; x++)
{
// Step 1: 중심점 기준 상대 좌표
double dx = x - cx;
double dy = y - cy;
// Step 2: 거리(r) 계산
double r = Math.Sqrt(dx * dx + dy * dy);
// Step 3: 정규화 (0.0 ~ 1.0)
// (0이면 나누기 에러가 나므로 1.0으로 처리)
double rNorm = (maxRadius == 0) ? 0 : r / maxRadius;
if (rNorm == 0)
{
indexerX[y, x] = x;
indexerY[y, x] = y;
continue;
}
// Step 4: 왜곡 적용 (Exponential)
double rNew = Math.Pow(rNorm, exp);
// Step 5: 비율 계산 (Scale Factor)
// 삼각함수(atan2, sin, cos) 없이 비율만으로 좌표 유추 -> 고속화
double scaleFactor = rNew / rNorm;
// Step 6: 원본 좌표 매핑
// "원래 거리보다 비율만큼 더 멀리(또는 가까이) 있는 픽셀을 가져와라"
float srcX = (float)(cx + dx * scaleFactor);
float srcY = (float)(cy + dy * scaleFactor);
// 매핑 테이블에 저장
indexerX[y, x] = srcX;
indexerY[y, x] = srcY;
}
});
// 3. Remap 실행 (보간법 적용)
Cv2.Remap(_srcImage, _destImage, mapX, mapY, InterpolationFlags.Linear);
// 리소스 해제
mapX.Dispose();
mapY.Dispose();
resultMessage += $": Lens Distortion (Exp: {exp:F2})";
}
else
{
// (기존 Wave 모드 코드는 생략)
}
}
break;실행 및 이미지 분석
이제 빌드 후 실행해 보겠습니다. Lens Distortion(렌즈 왜곡)을 이용한 이미지의 볼록 왜곡 효과와 오목 왜곡 효과는 이전 포스팅과 같이 동작합니다. 위 코드로 변경 후 동일한 이미지를 가지고 진행해 보세요. 동일하게 동작하는지 확인해 보시면 됩니다. 그리고 큰 이미지가 있다면 두 방식을 번갈아 가면서 테스트 했을 때 체감 하는 처리 속도도 한번 느껴 보시기 바랍니다.
자 정리하고 갈게요. 이번 포스팅에서 구현한 방식을 사용하면 지난 포스팅(#26)과 시각적으로는 동일한 결과를 얻지만, 내부적으로는 훨씬 효율적입니다.
- 메모리 절약: 불필요한
Mat객체 생성을 최소화했습니다. - 속도 향상:
Parallel.For를 통한 병렬 처리와 삼각함수(sin,cos) 제거를 통해 대용량 이미지에서도 쾌적하게 동작합니다. - 명확한 제어: 중심점, 왜곡 계수, 스케일 등을 수식 내에서 직관적으로 제어할 수 있습니다.
사실 이거 저것 생각 안하고 OpenCV에서 제공하는 라이브러리만 잘 가져다 써도 큰 문제를 발생하지 않지만, 단순히 라이브러리를 가져다 쓰는 것을 넘어, 알고리즘을 이해하고 최적화할 수 있는 수준에 도달한 것 같지 않아요?
다음에는 기하학적 변환의 마지막으로 카메라의 방사 왜곡(barrel distortion)에 대해 다루려고 합니다. 아마도 영상 처리를 이용한 검사 장비에서는 시스템 셋업 과정에서 반드시 한번은 수행하게 되는 Camera Calibration 입니다.
참고 자료
[Post #26] 렌즈 왜곡 기초: [WPF OpenCV Project #26] – Barrel & Pincushion 시각적 이해
Radial Distortion Model: Wikipedia – Distortion (Optics) – 방사 왜곡의 수학적 모델
Image Remapping: OpenCV Docs – Remap – 재배치 함수 원리